 Dipl. inž. Goran Marjanović: Razumevanje struktura čija je dimenzionalnost veća od tri izuzetno je teško iz prostog razloga što ih nema u našem čulnom iskustvu. Ipak, Realnost je sasvim nesumnjivo višedimenzionalna i svi problemi klasično-naučne misli proističu iz nerazumevanja stvarne suštine prostor-vremena a ona se može razumeti isključivo razmatranjem višedimenzionalnih, ne-euklidskih (zakrivljenih), struktura. Pokušaćemo zato da se upoznamo sa osnovnim pojmovima i osobinama najosnovnijih topoloških struktura.
Dipl. inž. Goran Marjanović: Razumevanje struktura čija je dimenzionalnost veća od tri izuzetno je teško iz prostog razloga što ih nema u našem čulnom iskustvu. Ipak, Realnost je sasvim nesumnjivo višedimenzionalna i svi problemi klasično-naučne misli proističu iz nerazumevanja stvarne suštine prostor-vremena a ona se može razumeti isključivo razmatranjem višedimenzionalnih, ne-euklidskih (zakrivljenih), struktura. Pokušaćemo zato da se upoznamo sa osnovnim pojmovima i osobinama najosnovnijih topoloških struktura.
Površina je pojam koji asocijativno vezujemo za dvodimenzionalne objekte kakav je npr. krug a zapremina je pojam koji odgovara trodimenzionalnim strukturama kakva je npr. lopta. Ipak, u topološkom smislu ovi pojmovi imaju šire značenje što je ilustrovano sledećom tabelom:
Kada je reč o zakrivljenim topološkim oblastima, one predstavljaju “površinu” posmatrane strukture i dobijaju se izvodom njene topološke zapremine. Ukoliko je broj dimenzija tri, pojam topološke zapremine podrazumeva (Euklidsku) strukturu V3 i za N=3 to je lopta. Njena topološka površina podrazumeva (Riemanovsku) strukturu S2, odnosno dvodimenzionalni kontinuum zatvoren u samog sebe kao što je to npr. površina lopte, torusa i sl., i to nam nije teško zamisliti.
Ukoliko “zavirimo” u svet sa dimenzijom manje (N=2), topološka “površina” podrazumeva strukturu S1 opisanu izrazom 2πr, što predstavlja kružnicu. U realnom svetu – to je npr. ekvator.
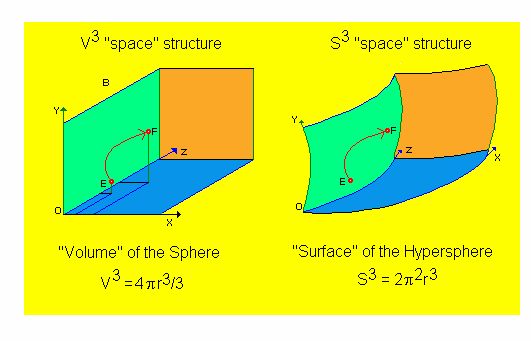
Porastom broja dimenzija na četiri – stvari se znatno komplikuju i za tako nešto potrebna je izuzetno bogata mašta i velika moć imaginacije. Kao pomoć u razumevanju višedimenzionalnih zakrivljenih struktura može nam poslužiti ilustracija na kojoj se porede V3 i S3 strukture. Obe su trodimenzionalne topološke oblasti s tim što postojanje S3 strukture podrazumeva apriori i realno postojanje neke četverodimenzionalne strukture čija je ta S3 oblast topološka “površina”.
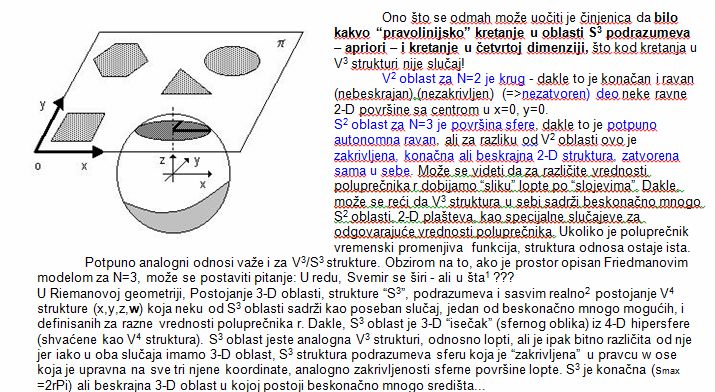
Za razliku od nje, S3 struktura istog objekta, predstavlja 3-D sferu čija se svaka tačka može opisati sa tri koordinate: x, y i z, ali sferu koja je “zakrivljena” u pravcu ose w (koja je upravna na sve tri koordinate, u svim proizvoljno odabranim tačkama S3 oblasti). Ovako definisana sfera, predstavlja Riemanovu 3-D oblast koja je konačna (najduži mogući put bez ponavljanja je s=2rPi) ali beskrajna struktura, zatvorena sama u sebe, u kojoj postoji beskonačno mnogo tačaka koje se mogu izabrati kao njeno središte, sasvim analogno “centru” proizvoljno izabranog kruga na sfernoj površini neke lopte. Takvih “površinskih krugova” (pod-domena strukture S2) proizvoljnog poluprečnika r, može postojati proizvoljan broj, ali centar lopte (strukture V3) čiji je prečnijk R može postojati samo jedan, pri čemu su SVI prečnici “površinskih krugova” r upravni na prečik lopte R, odnosno, ako zamislimo da se neki od tih zamišljenih “površinskih krugova” kreće (kroz svoj 2D svet) po površini lopte njegov je prečnik r UVEK upravan na prečnik lopte R. Isto važi i za dimenziju više. Proizvoljno odabrani prečnik bilo koje, takodje proizvoljno odabrane sfere u okviru domena S3 – uvek je upravan na prečnik svoje V4 strukture.
Analogno prethodnom primeru, gde smo rotiranjem kruga dobili sferu, u topološkom smislu, hipersfera se može dobiti “rotiranjem” V3 oblasti sfere oko bilo koje ose tog domena u pravcu upravnom na tu osu, dakle rotiranjem sfere upravno na sebe samu.
 Može li se ovo grafički predstaviti? Pokušajmo prvo, u dimenziji niže, u ravnom 2-D prostoru tipa V2, kakav je recimo zemljopisna karta, opisati zakrivljenu sfernu površinu Zemlje koja je po svojoj strukturi nesumnjivo tipa S2, dakle trodimenzionalna zakrivljena površina.
Može li se ovo grafički predstaviti? Pokušajmo prvo, u dimenziji niže, u ravnom 2-D prostoru tipa V2, kakav je recimo zemljopisna karta, opisati zakrivljenu sfernu površinu Zemlje koja je po svojoj strukturi nesumnjivo tipa S2, dakle trodimenzionalna zakrivljena površina.
Jedan od mogućih “opisa” je (The Standard Mercator Projection) onaj koji dobijamo posmatranjem iznad ekvatora, iz svih tačaka oko Zemlje, što je prikazano na slici levo.
Sasvim je jasno da je projekcijom zakrivljene S2 oblasti na potpuno ravnu V2 strukturu, izvorna, realna slika prilično deformisana “umetanjem praznina” koje su proporcionalne razlici u realnom položaju tačaka u “dimenziji više”, tako da su one najveće na polovima dok ih na samom ekvatoru uopšte nema. Ipak, slika je prilično verna izvornoj, imajući na umu da su horizontalni razmaci tačaka na polovima višestruko uvećani. Dakle, u ovakvoj 2-D projekciji, geografska širina je realna dok su objekti prividno razmaknutiji što su bliže polovima. U principu, cela gornja (braon) linija, kao i donja (plava) iz naše V2 strukture, zapravo su tačka (severni i južni pol) u realnoj S2 strukturi Zemljine površine.
Postoji još jedan način na koji se 3-D (zakrivljena) površina Zemlje može prikazati u (nezakrivljenoj) 2-D formi, dakle u “ravnom svetu” sa dimenzijom manje.
Ako primenimo polarnu projekciju (The Polar Projection) posmatrajući povšinu Zemlje iznad svakog od geografskih polova dobijamo dve slike, sliku severne i sliku južne hemisfere:
Ova projekcija ima slične nedostatke kao i Merkator projekcija. U ovom slučaju naime, realna, zakrivljena površina Zemlje koju prikazujemo u 2-D ne-zakrivljenoj formi, je utoliko deformisanija ukoliko smo bliže ekvatoru, s tim da se ovaj put greška javlja u geografskoj širini. Ovde je dakle geografska dužina realna dok posmatranjem iz tačaka polova u pravcu ekvatora imamo iluziju “kontrakcije dužine” proporcionalnu približavanju ekvatoru.
Dakle, površina sfernog oblika, koja ima trodimenzionalnu, zakrivljenu strukturu oblika S2 može se, u najvećem delu i prilično verno, opisati pomoću dve prividno odvojene V2 oblasti.
Veoma je važno uočiti da se visinske koordinate tačaka koje realno postoje u strukturi V3 (planine, doline …) u topološkim kartama opisuju različitim bojama pri čemu svaka boja odgovara odredjenoj “visini”, odnosno “dubini” i predstavlja ravan paralelnu površini Zemlje, odnosno fiktivnu sferu tipa S2 sa prečnicima koji odgovaraju odabranoj nadmorskoj visini/dubini.
Nema nikakve dileme da je ekvator kružnica (S1) čiji je prečnik jednak prečniku Zemlje, skup tačaka koje su zajedničke za obe hemisfere (rS1=rS2), iako na našoj dimenziono nižoj, “dvo-kružnoj” (V2) projekciji objekta (koji realno ima V3/S2 strukturu) uopšte ne izgleda tako. Ipak, jasno je da rubne oblasti oba kruga predstavljaju neprekinutu, kontinuiranu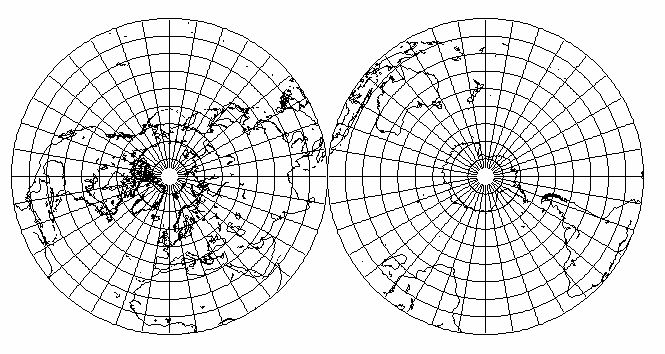 oblast u kojoj sve tačke koje mi vidimo kao krajnje, rubne tačke svake od hemisfera, u (višoj) realnosti (S2/V3) zapravo imaju jednu istu, sasvim identičnu poziciju – oblast S1 – koja je zajednička za obe hemsfere!
oblast u kojoj sve tačke koje mi vidimo kao krajnje, rubne tačke svake od hemisfera, u (višoj) realnosti (S2/V3) zapravo imaju jednu istu, sasvim identičnu poziciju – oblast S1 – koja je zajednička za obe hemsfere!
Pojasnimo ovo još malo.
Na gornjoj slici je ilustrovana projekcija S2 strukture (3-D “površina”) na V2 strukturu (2-D “zapremina”), sasvim analogno prethodnom primeru sa Zemljom, samo su ovde uklonjeni kontinenti.
Kako smo videli u prethodnom odeljku, sferna površina oblika S2 je zakrivljena 3-D forma ali je mi ipak možemo prikazati ortogonalnom projekcijom na 2-D strukturu oblika V2, pri čemu moramo koristiti dve odvojene oblasti strukture V2, kako bi mogli prikazati (približan) izgled obe hemisfere. Na jednoj dobijamo projekciju iz bilo koje proizvoljno odabrane tačke u strukturi S2, a druga se dobija posmatranjem iz antipoda te tačke. Očito je dakle, da se kontinuirana sferna oblast mora podeliti na dve različite komponente – “severnu” i “južnu” hemsferu sa neizbežnim “prekidom” na ekvatoru.
Na slici gore, možemo videti prikaz četiri različite trajektorije: A, B, C, i D , od tačke severnog pola preko južnog i nazad u polaznu tačku. Indeks 1 imaju sve one tačke u kojima se napušta severna hemisfera i ulazi u oblast južne, a tačke u kojim se ponovo vraćamo u oblast severne hemisfere imaju indeks 2.
Iako (posmatrajući projektovanu sliku) izgleda da oblasti V2 imaju samo jednu zajedničku tačku – C1, dok izmedju ostalih postoji totalni diskontinuitet i izgleda kao da su to potpuno različite tačke, jasno je da oba kruga iz naših V2 projekcija pripadaju istoj, potpuno kontinuiranoj oblasti S2, tako da sve tačke sa istim indeksom zapravo imaju ISTU poziciju (ekvator) u strukturi S2. Pri tome, u momentu kada prelaze ekvator (S1; rS1=rS2), sve trajektorije su paralelne i sve one (N,C1,S,C2,N; N,A1,S,A2,N; ..) imaju istu ukupnu dužinu od 2rπ.
Pokušajmo sada primeniti iste principe u dimenziji više.
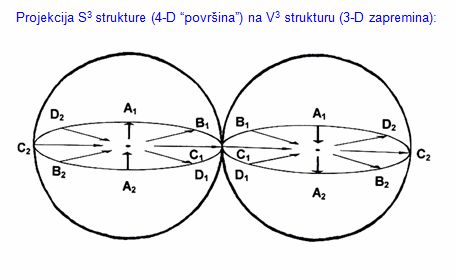
Trodimenzionalna zapremina (“površina” hipersfere) oblika S3 takodje je zakrivljena na sličan način, pa analogno prethodnom primeru sa sferom, ovaj zakrivljeni (S3) hiper-prostor možemo podeliti u dve odvojene “hemi-hipersfere” tako da svaku od njih možemo projektovati[1] u po jednu formu klasičnih 3D sfera strukture V3, što je ilustrovano sledećom slikom:
Da bi zadržali do sada uspostavljene analogije, i ovde su prikazane odgovarajuće trajektorije i označene na identičan način, uz korištenje istih konvencija (vezano za indekse), s tim što sada pokušavamo opisati projekciju jedinstvene S3 strukture na dve (prividno) odvojene oblasti oblika V3.
I ovde, baš kao i u slučaju dveju hemisfera iz prethodnog primera, obe sfere, prikazane na gornjoj slici, su kontinuirane u svim lokacijama[2] “površine” S3 koju predstavljaju. Isto tako, i potpuno analogno prethodnom slučaju, sve trajektorije su potpuno paralelne kada prelaze iz jedne u drugu, “suprotnu”, hemi-hipersferu.
Ovakva dvo-sferna konfiguracija (double bubble) ilustruje hipersferu sa istom aproksimacijom sa kojom dva kruga (V2) opisuju zakrivljenu sfernu površinu tipa (S2), dakle na dovoljno prihvatljiv način. Ipak, imajući u vidu da je ovo analogija polarne projekcije, moramo imati na umu da je ovde greška najmanja u centrima V3 domena a najveća u njihovim rubnim oblastima.
Obzirom na našu pretpostavku da se svetlost realno prostire kroz S3 strukturu (3-D sfernu, zakrivljenu, beskrajnu ali konačnu oblast – “površinu” – hipersfere) dok mi vidimo/merimo samo njenu projekciju u naš dvo-sferni, V3-strukturni 3-D svet, uvek kada gledamo iz jedne tačke hipersfere ka njenoj 4-D “suprotnosti” duž (kroz) njene(u) “površine” S3, to se u našu dvo-sfernu aproksimaciju projektuje kao posmatranje iz centra jedne sfere ka centru one druge, “suprotne” sfere – ma gde gledali unutar neke od sfera. Centar te druge, suprotne sfere (V3) je projekcija “4-D antipoda” hipersfere. To je najudaljenija tačka od neke proizvoljne pozicije u strukturi S3, pre nego što naša trajektorija, tj. “linija gledanja” od nas ka antipodu, počne da menja smer u nazad – od antipoda ka nama. Rubna oblast obeju sfera (“plašt”) u našoj dvo-sfernoj V3 projekciji odgovara S2 oblasti tako da su rSf1 i rSf2 = rS2 = rV3. U strukturnom smislu prelaz sa jedne hemi-hipersfere na onu drugu analogan je prelazu sa južne na severnu (ili obrnuto) hemisferu Zemlje, što se u našoj dvo-sfernoj V3 projekciji vidi kao prelaz iz jedne u drugu sferu.
Baš kao što putanja oko sfere, uz konstantan poluprecnik r ima vrednost 2rPi, tako da je udaljenost neke tačke do svog 3-D antipoda rPi, na isti način je kod hipersfere udaljenost antipoda takodje rPi.
Naravno, ono što mi možemo videti kao projekciju u našu V3 strukturu, znatno se razlikuje od stvarne slike – dogadjaja u S3.
Podsetimo se – da bi uspostavili analogiju sa 2-D prikazom 3-D sferne površine Zemlje, podelili smo Zemlju na severnu i južnu hemisferu, imajući na umu da je ekvator kružnica koja pripada obema hemisferama a sve tačke na ekvatoru su sastavni deo neprekinutog S2 kontinuiteta obeju hemisfera. Na isti način, pri podeli hipersfere na dve “hemi-hipersfere”, w koordinata može imati vrednost od 0 do pozitivne vrednosti r u slučaju “gornje” hemi-hipersfere, ili od 0 do negativne vrednosti r u slučaju “donje” hemi-hipersfere. U oba slučaja, x,y i z koordinate mogu imati proizvoljne vrednosti u opsegu -r do +r. Obzirom da w promenjiva može imati vrednost 0 u oba slučaja, iz funkcije (3) koja opisuje hipersferu, za w=0 dobija se jedinstveno rešenje za obe hemi-hipersfere:
Obzirom da pretpostavljeno kretanje oblika (4) podrazumeva prostorno-vremenske promene, podrazumeva se da i pojam projektovane “fazne” razlike takodje ima sasvim identičnu strukturu (fazna razlika je takodje prostrono-vremenska, npr. EPR efekat, teleportacija …).
1. mogućnost: realno V4 kretanje se odvija u istoj hemi-hipersferi u kojoj se nalazi i posmatrač.
Ukoliko se realno V4 kretanje projektuje u istu hemi-hipersferu u kojoj smo “smešteni” i mi kao posmatrači, onda svakoj tački sa koordinatama x,y,z,w, odgovaraju “senka” tačke x’,y’,z’ uz w=0 (analogno polarnoj projekciji na ravan ekvatora). Sasvim je jasno da promena položaja tačke unutar V4 strukture u smeru w koordinate u našem svetu može biti opisana samo prikazom u formi različitih sfernih struktura – gde je svaka do njih opisana istim x,y i z koordinatama ali svakoj od njih odgovara druga vrednost koordinate w, pa dakle ima i drugačiju vrednost poluprečnika r(V4/S3) koju je nemoguće uočti u V3 prostornoj formi, ali se u S3 strukturi može shvatiti kao njena manja ili veća zakrivljenost (0<r<R). Analogija sa topografskim “trikom” sa bojama pri opisu treće koordinate iz S2 oblasti Zemlje pri njenoj projekciji na V2 strukturu zemljopisne karte je potpuna. Kako smo videli, u slučaju V3/S2 strukture (Zemlja) imamo “babuška-sistem” zakrivljenih sfernih površina oblika S2 sa različitim vrednostima prečnika r(V3/S2), koje u stvari odgovaraju različitim nadmorskim visinama neke tačke sa identičnim x i y koordinatama. Analogno tome, imajući na umu da mi kao projekciju iz V4 strukture možemo percipirati samo različite forme oblika V3 (projekcije S3), ovde imamo “babuška sistem” zakrivljenih struktura S3 sa različitim prečnicima r(V4/S3), što se u našoj V3 “realnosti” manifestuje (projektuje) kao tačka sa identičnim x, y i z koordinatama pri čemu svaka od njih pripada V3 sferi sa različitim prečnikom r, odnosno drugoj S3 strukturi sa drugačojom zakrivljenošću (u pravcu w koordinate)…
Ovo se najpribližnije može opisati kao kretanje neke tačke upravno na sve tri koordinate (x,y i z), dakle u pravcu “ka izvan” i “na unutra” u odnosu na samu sebe, pri čemu vrednosti njenih x, y, i z koordinata ostaju nepromenjene.
Dakle, 4D kretanju nekog objekta iz tačke T1 sa koordinatama x1, y1, z1, w1 do tačke T2 sa koordinatama x2, y2, z2, w2 na “nama odgovarajućoj hemi-hipersferi” neke V4 strukture, odgovara 3D projekcija tog kretanja u “našu” V3 sferu od tačke T1’: x1’, y1’ i z1’, uz r(V4/S3), za w=w1 do tačke T2’: x2’, y2’ i z2’, uz r(V4/S3), za w=w2. Uz usvojene konvencije jasno je da, iako tačke T1’ i T2’ pripadaju istoj V3 strukturi, u kojoj je nemoguće iskazati različitost u smeru w ose izuzev pomoću neke “novo-uvedene” kategorije različite od x,y, i z kvalteta, one pripadaju potpuno različitim S3 oblastima, gde se promena položaja po w osi sasvim jednostavno opisuje promenom u pravcu poluprečnika njene zakrivljenosti, dakle kategorijom koja je potpuno srodna x, y i z kvalitetima!
Očito je naime da tačke T1’ i T2’, iako u smislu Riemanove geometrije pripadaju istoj V3 strukturi, pripadaju zapravo sasvim različitim S3 oblastima, koje mi, u skladu sa usvojenim konvencijama, opisujemo kao “projekcije” u formi V3 sfera koje imaju svaka svoj prečnik. Tački T1 odgovara sfera prečnika r1(V4/S3), za w=w1 a tački T2 odgovara sfera prečnika r2(V4/S3), za w=w2. Prema tome, tačka koja se u svom realnom V4 sistemu kreće linearno u pravcu ose w uz x,y z = const, (u smislu S4 strukture to je opet konačno, zakrivljeno i samo u sebe zatvoreno kretanje), projektuje se u naš V3 prostorni sistem kao mirovanje u smislu x,y i z koordinata ali i kao sferno kretanje po “babuška sistemu” (“unutar-izvan”) pri čemu objekat prividno miruje u V3 strukturi a prečnik odgovarajuće S3 sfere predstavlja projekciju w koordinate u taj domen. Odavde je sasvim lako vidljivo da vektor kretanja u pracu w ose unutar V4 strukture ima smisao promene zakrivljenosti odgovarajuće S3 oblasti što mi unutar svoje vlastite V3 strukture možemo meriti samo kroz odgovarajuće deformacije V3 projekcija (npr. kontrakcija dužine u pravcu kretanja …; r V3 <> const => EMT …).
2. mogućnost: realno V4 kretanje se projektuje u hemi-hipersferu supotnu onoj u kojoj se nalazi posmatrač.
Ukoliko se realno V4 kretanje “dešava” na suprotnoj hemi-hipersferi u odnosu na naš 4D položaj kao posmatrača, onda je to u dvo-sfernoj V3 projekciji analogno posmatranju iz ”naše” sfere V3 strukture (naša “poluslika” – dvo-sferne projekcije S3) gde smo smešteni i mi kao posmatrači, nekog dogadjaja koji se dešava u onoj “drugoj sferi” (V3) čiji je centar antipod centra naše sfere. Sasvim je jasno da svakoj tački sa koordinatama x,y,z,w, odgovaraju “senka” tačke x’,y’,z’ uz w=0 (analogno polarnoj projekciji na ravan ekvatora), ali za razliku od slučaja 1, gde su sve tačke x,y,z,w projektovane u domen w = 0, u realnoj 4D strukturi pripadale skupu u kojem je koordinate w imala vrednost od 0 do +r, sada imamo projekciju na isti domen w=0 ali “odozdo”, iz oblasti u kojoj koordinata w ima opseg vrednosti od 0 do –r. Dakle, dok smo u slučaju 1) posmatrali dogadjaj na istoj hemi-hipersferi, kojoj je odgovarala “unutrašnja” S3 oblast sa konkavnim kvalitetama, u ovom slučaju posmatramo dogadjaj na suprotnoj hemi-hipersferi kojoj odgovara ona “druga” – “vanjska ”S3 oblast koja (za nas) “ima” konveksnu formu.
Obzirom na sve rečeno kao i definiciju datu izrazom (6), očito je da će bilo kakvo realno 4D kretanje na suprotnoj hemi-hipersferi posmatrano ili mereno iz bilo koje “naše” referentne tačke imati sasvim drugačiju prostor-vreme formu. Ukratko, dogadjaj – objekat će u našu V3 kvazi-realnost biti projektovan tako da će, za nas kao posmatrače, imati sasvim drugačiji izgled uključujući potpuno “inverzne” forme svih onih kategorija koje se u našoj V3+T strukturi manifestuju kroz pojam vreme.
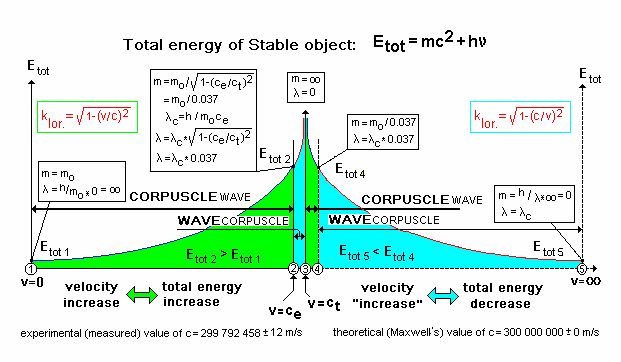
Da bi uočili suštinsku razliku izmedju naših shvatanja i klasično naučnih tumačenja pogledajmo ilustraciju Specijalne teorije relativnosti sa aspekta modela KGE i VOS.
Levi deo dijagrama od tačke 1 do tačke 3 je dijagram kakav nudi klasična nauka i na koji se ovaj svodi ako usvojimo ce = ct = c, što smatramo najvećom zabludom savremene nauke i njenom najvećom preprekom u uskladjivanju osnovnih postavki T.R. i Q.T sa objektivnom stvarnošću, o čemu svedoče svi najnoviji eksperimenti i njihova tumačenja.
Energetski “prozor” izmedju tačaka 2 i 3 koji nam nudi i otvara model KGE, odnosno hipoteza 3, mali je samo u kvantitativnom smislu (ce = 299 792 458; ct = 3*108 m) dok nam u kvalitativnom nudi jedan sasvim novi pogled na svet, u smislu “drugačijeg vidjenja ISTOG”. Zapravo, dilemu čestica ili talas, nauka je davno razrešila kao “čestica i talas” ali više deklarativno jer “most” izmedju čestice i talasa nikada nije “izgradjen”.
Naš model je sasvim odredjen i jasan. Ne postoji “jedno energetsko stanje” koje se može, u zavisnosti od uslova (okoline) iskazivati na dva različita “načina”, kao dva različita “objekta”, čestica ili talas, pri čemu objekat može biti jedno ili drugo, iskazujući tako svoju dualističku prirodu, što je klasično naučno tumačenje, nego JEDAN (stabilni) OBJEKAT, čestica-talas, koji može imati DVA kvalitativno RAZLIČITA ENERGETSKA STANJA, pri čemu, vidjenje JEDNOG ISTOG objekta, po strukturi česticatalasa, kao čestice(talasa) ili talasa(čestice) zavisi i od energetskog stanja njegove okoline, odnosno lokalne sredine (i u smislu specijalne i u smislu opšte teorije relativnosti)! U prilog toj ideji navodimo činjenicu da je porast mase u tački 2 “svega” oko 27 puta! ( za v=ce/2 porast mase je 15.47 %, a za v=ct/2 oko 15.44 %, što je i za tako velike, čoveku za sada nedostižne brzine, zanemariva razlika, i što ukazuje na činjenicu da se “prave stvari”, relevantne za naš svet dešavaju tek pri brzinama VEOMA bliskim brzini svetlosti). Sve što se nalazi u opsegu od tačke 2 pa do tačke 3, za klasičnu nauku jednostavno ne postoji a vrednosti za v > c (ce=ct=c), SU IMAGINARNE VELIČINE ! Zavirimo u novi svet, svet sa “one strane” luksonskog zida, koji nam otvara model KGE.
Posmatrač koji se nalazi sa “ove strane”, u “energetskom stanju” bliskom tački 1, objekat A čija je brzina kretanja manja od eksperimentalno izmerene brzine svetlosti, v < ce, neki mirujući ili sporo pokretni objekat vidi kao česticu(talas) realno-merljive mase i poluprečnika, sa odgovarajućom talasnom dužinom, takodje realnom ali zanemarivo malom i nama teško merljivom veličinom, pa ga on doživljava kao česticu. Porastom brzine kretanja, raste i masa objekta A, odnosno njegova totalna energija, bez obzira na to da li ju mi iskazujemo kao porast mase ili kao smanjenje pripadajuće talasne dužine. U zavisnosti od mase mirovanja, približavanjem tački 2, raste vrednost talasne dužine objekta A, pa će ona pre ili kasnije dobiti opažljivo-merljivu vrednost, pri čemu posmatrač (tek) tada uočava dualističku prirodu tog objekta. Kada objekat A prevazidje brzinu ce pri čemu je ona manja od ct, posmatrač iz stanja 1 ga doživljava kao neki sasvim drugi objekat (u kvalitativnom smislu), kao objekat talasne prirode, jer mu njegova masa postaje neperceptibilna u bilo kom smislu, a talasna dužina sasvim realno – merljiva veličina!
Uz terminologiju koju smo usvojili razmatranjem višedimenzionalnih topoloških oblasti, sada možemo reći da objekat koji miruje ili se kreće malom brzinom iz svoje («severne» npr.) hemi-hipersferne strukture NEmože preći u onu «drugu» («južnu») hemi-hipersferu proizvoljno dugim kretanjem, takodje proizvoljnom ali pod-svetlosnom brzinom – nego isključivo prekoračenjem brzine svetlosti (u skladu sa H3 modela KGE). Iako objekat ostaje unutar istog V4/S3 domena, za nas kao posmatrače on menja formu iz predominantno čestične u predominantno talasnu i obrnuto.
U narednom broju: “Vreme” kao inverzno-opozitna struktura “prostora” (P.D. Uspenski)
Trodimenzionalno vreme http://kpv.rs/?p=1977#more-1977
[1] Veoma je važno imati na umu da ovaj proces podrazumeva postojanje greške u prikazu IV dimenzije tako da su svi naši 3D «prikazi» deformisani, sasvim analogno grešci koja se javlja pri prikazu (projekciji) S2 strukture (3-D “površina” Zemlje) na V2 strukturu (2D zemljopisna karta).
[2] Oblast kontinuiranosti “Površine” S3 ima strukturu S2 koja predstavlja zakrivljenu sfernu površinu (površina lopte) i sasvim je analogna pojmu ekvatora, topološke strukture oblika S1.









 u
u 




Genijalno, zaista! Svaka čast! Ovaj je možda čak i najbolji, odnosno da budem precizniji – svaki je sve bolji i bolji! Genijalnost se brusi i upravo, poštovani Gorane, dolazite do toga. Odraz je originalnost i analogija!
Moram priznati da imam problema sa razumevanjem sadržaj ovog teksta, odnosno pitam se – da li bi objašnjenje njegovog sadržaja moglo da bude prijemčivije, jednostavnije? … I čini mi se da ne bi, da je tema takva-kakava-je, višedimenzino uvijena u samu sebe.
Svidja Mi Se