Kretanje planeta oko Sunca oduvek je izazivalo divljenje i predstavljalo misteriju i udaljenost planeta od Sunca je problem koji do danas nije egzaktno definisan dok je Titius-Bodeov zakono zapravo samo empirijski obrazac.
Piše: Milun Dimić

U ovom radu je učinjen napor da se naučno objasni i definiše odstojanje planeta od centra rotacije, objasni razlog eliptičnih putanja planeta i dokaže postojanje restitucionih prostora koji drže planete na rotacionim putanjama.
Rad je nastavak (drugi deo ) rada POREKLO BROJEVA , DIMENZIJE PLANETA I GRANICE PROSTORA.
U prvom delu (ponenutog rada) definisane su ORBITE SUNCA, odredjen njihov broj (30), i odredjen postupak izracunavanja srednje vrednosti udaljenosti planeta i satelita od centra rotacije.
U radu ROTACIONO HARMONIJSKO OSCILOVANJE, objašnjen je razlog eliptične putanje planeta pri rotaciji , i odredjen postupak izračunavanja trenutne udaljenosti planeta od centra rotacije.
U radu je uočena činjenica postojanje restitucionih polja oko centra rotacije.
Zaključak:
1.Planete koje se kreću oko centra rotacije periodično, su harmonijski oscilatori.
2.Harmonijsko oscilovanje je uslovljeno postojanjem restitucionih sila, na osnovu izloženog matematičkog modela harmonijskog oscilatora kojeg mi poznajemo.
3.Ako su planete pri svom kretanju izložene dejstvu restitucionih sila, onda postoje restituciona polja (prostori), po kojima se planete kreću.
4.Planete se oko centra rotacije kreću po sferama ciji je poluprecnik dat jednacinom (3) i koji odredjuje udaljenost planete od centra rotacije.
Pojave kao sto su kretanja planeta, noc i dan, itd. su periodične pojave.
Harmonijsko oscilovanje je jedna vrsta periodičnog kretanja.
Najednostavniji primer harmonijskog oscilovanja je linearno harmonijsko oscilovanje pod dejstvom sile koja je srazmerna udaljenosti tela od ravnotežnog položaja , restitucione sile F = -kx , gde je k-konstanta opruge i x-udaljenje od ravnotežnog položaja
Model oscilatora
Telo mase m prikačeno je na oprugu konstante elasticnisti , k, i klizi bez trenja po horizontalnoj ravni.
Polozaj označen tačkom B je ravnotežni položaj.
Izvođenje tela iz ravnotežnog položaja vrši se istezanjem opruge do tačke C, ili sabijanjem opruge do tačke A.
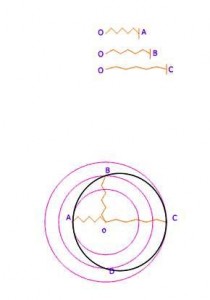
Telo rotirajući oko centra rotacije O prelazi put opisujući krivu od tacke A, B, C, D do A,ili A,D,C,B do A u zavisnosti od vrste rotacije.
Jednačina koja opisuje ovu vrstu kretanja data je:
m * (d2x/ dτ2) = – kx
ω2 = k/m
(d2x/ dτ2 )+ ω2 * x = 0
X (τ) = X0 sin (ωt + φ)………………………………………………………………………………………(1)
Ovom jednačinom su definisane vrednosti udaljenja mase ( m ) od ravnotežnog položaja tokom kretanja u zavisnosti od kružne frekvence i perioda oscilovanja.
Na priloženoj slici dat je model oscilatora koji rotira oko tačke O .
Odstojanje O A je najbliže odstojanje od centra rotacije ,Rmin
Odstojanje O B je srednje (ravnotežno) odstojanje od centra rotacije ,Rsr
Odsojanje O C je najdalje odstojanje od centra rotacije Rmax
Maksimalno udaljenje mase m od ravnoteznog polozaja definisano je
Xo = (Rmax-Rmin)/2 ………………………………………………………………………………………………(2)
U radu O POREKLU BROJEVA , DIMENZIJAMA PLANETA I GRANICAMA PROSTORA , jednačina (6) definiše način odredjivanja srednje udaljenosti planeta od centra rotacije (Sunca)
R sr = D/2*(exp(1/3))n.
gde je D-precnik Sunca i n -broj orbite po kojoj kruži planeta
Za planete Sunčevog sistema vrednosti za broj n su sledeće
Merkur n=13,26 , Venera n=15,139 , Zemlja n=16,12 , Mars n=17,37 , Jupiter n=21,05
Saturn n=22,88 , Uran n=24,97 , Neptun n=26,32 , Pluton n=27,14 , Erida n=29,83
MODEL PUTANJE PLANETE OKO SUNCA
–harmonijsko oscilovanje oko centra rotacije ili kretanje po elipsi-
Telo mase m pod dejstvom opruge klizi po horizontalnoj ravni bez trenja kao harmonijski oscilator i istovremeno rotira oko centra rotacije.Odstojanja od ravnoteznog položaja definisana su izrazom (1)
Odstojanje od Sunca definisano je izrazom
R=Rsr +X(t)
Udaljenost planete od Sunca sada definisana je izrazom
R=D/2*(exp(1/3))n +( (Rmax-Rmin)/2 )sin(ω+φ)……………………………………………………..(3)
Zaključak
Ako je kretanje planeta oko Sunca oblik harmonijslog oscilovanja, onda postoji restituciona sila koja definiše kretanje planete oko ravnotežnog položaja. Polje u kojem se oseća dejstvo ovih sila je RESTITUCIONO POLJE.
Ovo polje se prostire izmedju PERIHELA i AFELA .
Rotacioni harmonijski oscilator
SLIKA MODELA
MILUN DIMIĆ




 u
u 



